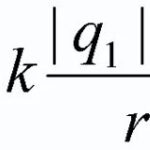Vládne Lorentzova síla a levá ruka. Pohyb nabitých částic v magnetickém poli

Umístěn v magnetickém poli dirigentpřes který prošel elektřina, je ovlivněna silou Ampere $F_A$ a jeho hodnotu lze vypočítat pomocí následujícího vzorce:

$F_A=B\cdot I\cdot l\cdot sin\alpha$ (1)

kde $já$ a $l$ - síla proudu a délka vodiče, $B$ - indukce magnetického pole, $\alpha$ - úhel mezi směry síly proudu a magnetické indukce. Proč se tohle děje?

Lorentzova síla. Pohyb nabité částice v magnetickém poli.

Obsah

1 Co je Lorentzova síla - určení, kdy nastane, získání vzorce
2 Určení směru Lorentzovy síly pomocí pravidla levé ruky
3 Pohyb nabité částice v magnetickém poli
4 Aplikace Lorentzovy síly ve strojírenství

Co je Lorentzova síla - určení, kdy nastane, získání vzorce

Je známo, že elektrický proud je uspořádaný pohyb nabitých částic. Bylo také zjištěno, že během pohybu v magnetickém poli je každá z těchto částic vystavena působení síly. Aby nastala síla, musí být částice v pohybu.

Lorentzova síla je síla, která působí na elektricky nabitou částici, když se pohybuje v magnetickém poli.Jeho směr je ortogonální k rovině, ve které leží vektory rychlosti částic a síly magnetického pole. Výsledkem Lorentzových sil je Ampérova síla. Když to víme, můžeme odvodit vzorec pro Lorentzovu sílu.

Čas potřebný k tomu, aby částice prošla segmentem vodiče, $t = \frac {l}{v}$ , kde $l$ - délka segmentu, $proti$ je rychlost částice. Celkový náboj přenesený během této doby přes průřez vodiče, $Q = I\cdot t$ . Když zde nahradíme časovou hodnotu z předchozí rovnice, máme

$Q = \frac {I\cdot l}{v}$ (2)

Ve stejný čas $F_A=F_L\cdot N$ , kde $N$ je počet částic v uvažovaném vodiči. V čem $N = \frac {Q}{q}$ , kde $q$ je náboj jedné částice. Dosazení hodnoty do vzorce $Q$ z (2), lze získat:

$N = \frac {I\cdot l}{v\cdot q}$

Takto,

$F_A=F_L\cdot \frac {I\cdot l}{v\cdot q}$

Pomocí (1) lze předchozí výraz zapsat jako

$B\cdot I\cdot l\cdot sin\alpha = F_L\cdot \frac {I\cdot l}{v\cdot q}$

Po kontrakcích a přesunech se objeví vzorec pro výpočet Lorentzovy síly

$F_L = q\cdot v\cdot B\cdot sin\alpha$

Vzhledem k tomu, že vzorec je napsán pro modul síly, musí být zapsán následovně:

Přečtěte si také: Jak převést zesilovače na watty a naopak?

$F_L = |q|\cdot v\cdot B\cdot sin\alpha$ (3)

Protože $sin\alpha = sin(180^{\circ} - \alpha)$ , pak pro výpočet Lorentzova silového modulu nezáleží na tom, kam směřuje rychlost, - ve směru síly proudu nebo proti, - a můžeme říci, že $\alpha$ je úhel tvořený vektory rychlosti částic a magnetické indukce.

Zápis vzorce ve vektorové podobě bude vypadat takto:

$\vec{F_L} = q\cdot [\vec{v}\times \vec{B}]$

$[\vec{v}\times \vec{B}]$ je křížový součin, jehož výsledkem je vektor s modulem rovným $v\cdot B\cdot sin\alpha$ .

Na základě vzorce (3) můžeme usoudit, že Lorentzova síla je maximální v případě kolmých směrů elektrického proudu a magnetického pole, tj. $\alpha = 90^{\circ}$ a zmizí, když jsou rovnoběžné ( $\alpha = 0^{\circ}$ ).

Je třeba mít na paměti, že pro získání správné kvantitativní odpovědi - například při řešení úloh - je třeba použít jednotky soustavy SI, ve které se magnetická indukce měří v teslach (1 T = 1 kg s⁻²·ALE⁻¹), síla - v Newtonech (1 N = 1 kg m/s²), síla proudu - v ampérech, náboj v coulombech (1 C = 1 A s), délka - v metrech, rychlost - v m/s.

Určení směru Lorentzovy síly pomocí pravidla levé ruky

Vzhledem k tomu, že Lorentzova síla se ve světě makroobjektů projevuje jako Ampérova síla, lze k určení jejího směru použít pravidlo levé ruky.

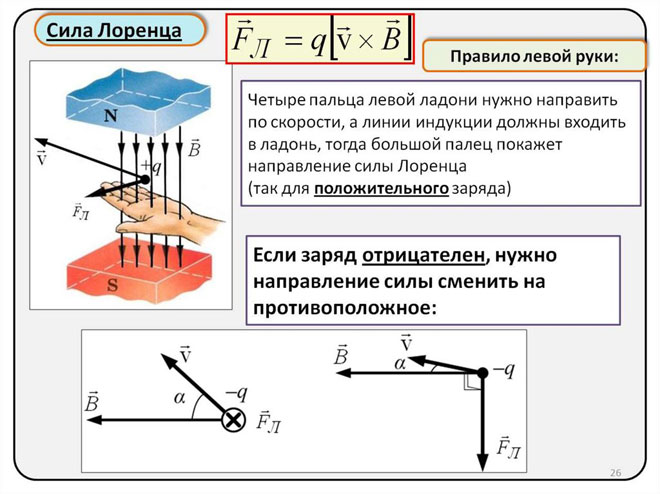
Určení směru působení Lorentzovy síly podle pravidla levé ruky.

Musíte položit levou ruku tak, aby otevřená dlaň byla kolmá k čarám magnetického pole a směrem k nim, čtyři prsty by měly být nataženy ve směru síly proudu, pak bude Lorentzova síla směřovat tam, kde ukazuje palec, který by měl být ohnutý.

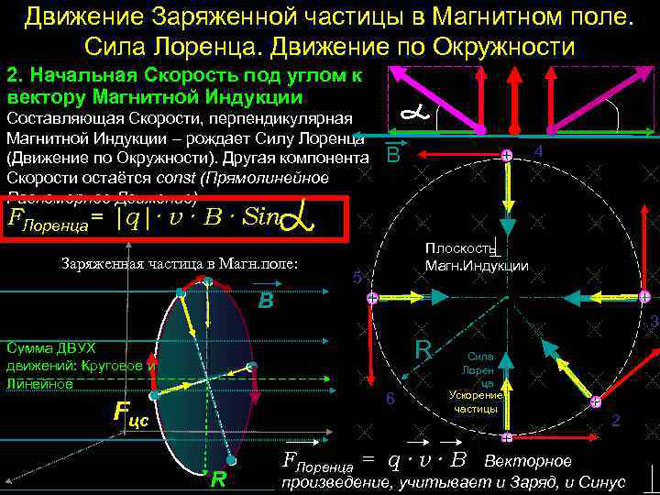
Pohyb nabité částice v magnetickém poli

V nejjednodušším případě, to znamená, když jsou vektory magnetické indukce a rychlosti částic ortogonální, může Lorentzova síla, která je kolmá k vektoru rychlosti, pouze měnit svůj směr. Velikost rychlosti a energie tedy zůstanou nezměněny. To znamená, že Lorentzova síla působí analogicky s dostředivou silou v mechanice a částice se pohybuje po kruhu.

Přečtěte si také: Kolik wattů je v kilowattu?

V souladu s Newtonovým zákonem II ( $F = m\cdot a$ ) můžeme určit poloměr rotace částice:

$N = \frac {m\cdot v}{q\cdot B}$ .

Je třeba poznamenat, že se změnou specifického náboje částice ( $\frac {q}{m}$ ) se mění i poloměr.

V tomto případě je doba rotace T = $\frac {2\cdot \pi\cdot r}{v}$ = $\frac {2\cdot \pi\cdot m}{q\cdot B}$ . Nezáleží na rychlosti, to znamená, že vzájemná poloha částic s různou rychlostí bude neměnná.

Pohyb nabité částice v rovnoměrném magnetickém poli.

Ve složitějším případě, kdy je úhel mezi rychlostí částice a intenzitou magnetického pole libovolný, bude se pohybovat po spirálové trajektorii - translačně v důsledku složky rychlosti nasměrované rovnoběžně s polem a po kružnici pod vlivem jejího kolmá složka.

Aplikace Lorentzovy síly ve strojírenství

Kineskop

Kineskop, který stál donedávna, kdy byl nahrazen LCD (plochou) obrazovkou, v každém televizoru, nemohl fungovat bez Lorentzovy síly. Pro vytvoření televizního rastru na obrazovce z úzkého proudu elektronů se používají vychylovací cívky, ve kterých vzniká lineárně se měnící magnetické pole. Horizontální cívky pohybují elektronovým paprskem zleva doprava a vracejí jej zpět, za vertikální pohyb jsou zodpovědné personální cívky, které pohybují paprskem probíhajícím vodorovně shora dolů. Stejný princip je použit v osciloskopy - přístroje sloužící ke studiu střídavého elektrického napětí.

hmotnostní spektrograf

Hmotnostní spektrograf je zařízení, které využívá závislosti poloměru rotace nabité částice na jejím specifickém náboji. Princip jeho fungování je následující:

Zdroj nabitých částic, které nabírají rychlost pomocí uměle vytvořeného elektrického pole, je umístěn ve vakuové komoře, aby se vyloučil vliv molekul vzduchu. Částice vylétají ze zdroje a po průchodu po oblouku kruhu narazí na fotografickou desku a zanechají na ní stopy. V závislosti na konkrétním náboji se mění poloměr trajektorie a tím i bod dopadu. Tento poloměr lze snadno změřit a pokud jej znáte, můžete vypočítat hmotnost částice. Pomocí hmotnostního spektrografu se například studovalo složení měsíční půdy.

Přečtěte si také: Jaké jsou profese související s elektřinou

Cyklotron

Nezávislost periody, a tedy i frekvence rotace nabité částice na její rychlosti v přítomnosti magnetického pole, se využívá v zařízení zvaném cyklotron a určeném k urychlení částic na vysoké rychlosti. Cyklotron jsou dva duté kovové půlválce - dee (tvarem každý z nich připomíná latinské písmeno D) umístěné rovnými stranami k sobě v krátké vzdálenosti.

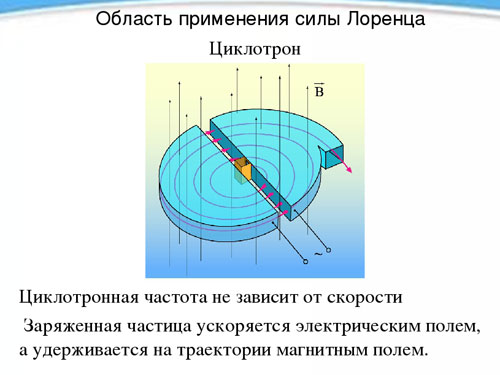
Cyklotron - aplikace Lorentzovy síly.

Dees jsou umístěny v konstantním stejnoměrném magnetickém poli a mezi nimi vzniká střídavé elektrické pole, jehož frekvence je rovna frekvenci rotace částice, určené intenzitou magnetického pole a měrným nábojem. Když se částice dostane dvakrát během periody rotace (během přechodu z jednoho dee do druhého) pod vlivem elektrického pole, pokaždé se zrychlí, zvětší poloměr trajektorie a v určitém okamžiku, když dosáhne požadované rychlosti, vyletí ze zařízení otvorem. Tímto způsobem lze proton urychlit na energii 20 MeV (megaelektronvolt).

Magnetron

Zařízení zvané magnetron, které je instalováno v každém mikrovlnná trouba, je dalším zástupcem zařízení využívajících Lorentzovu sílu. Magnetron slouží k vytvoření výkonného mikrovlnného pole, které ohřívá vnitřní objem trouby, kde je umístěn pokrm. Magnety obsažené v jeho složení korigují trajektorii pohybu elektronů uvnitř zařízení.

Magnetické pole Země

A v přírodě hraje Lorentzova síla pro lidstvo nesmírně důležitou roli. Jeho přítomnost umožňuje magnetickému poli Země chránit lidi před smrtícím ionizujícím zářením vesmíru. Pole neumožňuje nabitým částicím bombardovat povrch planety a nutí je změnit směr.

Podobné články: